Skip to content

Latest commit

 

History

History
1470 lines (1187 loc) · 44.4 KB

0xGame-2024-Crypto.md

File metadata and controls

1470 lines (1187 loc) · 44.4 KB
Raw

0xGame 2024-Crypto-Week 1

[Week 1] Caesar Cipher

  • 简单凯撒，偏移量为1
  • 0xGame{The_Beginning_Of_Crypto}

[Week 1] RSA-Easy

from Crypto.Util.number import *
from hashlib import md5
def MD5(m):return md5(str(m).encode()).hexdigest()
Pub_Key = (689802261604270193, 620245111658678815)
e = Pub_Key[1]
n = Pub_Key[0]
p = 823642439
q = 837502087
c = 289281498571087475
d = inverse(e,(p-1)*(q-1))
m = pow(c,d,n)
flag = flag = '0xGame{'+ MD5(m) +'}'
print(flag)
  • 0xGame{5aa4603855d01ffdc5dcf92e0e604f31}

[Week 1] Code

  • 逆向，编写脚本
from Crypto.Util.number import *
from base64 import b64decode
m0 = b'0xGame{73d7'
m1 = 60928972245886112747629873
m2 = '3165662d393339332d3034'
m3 = b'N2YwZTdjNGRlMX0='
m1 = long_to_bytes(m1)
m2 = bytes.fromhex(m2)
m3 = b64decode(m3)
print(m0+m1+m2+m3)
  • 0xGame{73d72f64-7656-11ef-9393-047f0e7c4de1}

[Week 1] Code-Vigenere

  • 由脚本可以知道key长度为5，恰巧0xGame正好五个字母
  • 编写脚本可以得到key是oWccl
alpha1 = 'abcdefghijklmnopqrstuvwxyz'
alpha2 = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
m = '0lCcop{oyd94092-g8mq-4963-88b6-4helrxdhm6q7}'
clue = '0xGame'
key = ''
for i in range(len(clue)):
    if clue[i] in alpha1:
        key += alpha1[(alpha1.find(m[i])-alpha1.find(clue[i]))%26]
    elif clue[i] in alpha2:
        key += alpha2[(alpha2.find(m[i])-alpha2.find(clue[i]))%26]
print(key)
  • 后续可以使用工具，或者使用脚本
alpha1 = 'abcdefghijklmnopqrstuvwxyz'
alpha2 = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
m = '0lCcop{oyd94092-g8mq-4963-88b6-4helrxdhm6q7}'
key = 'oWccl'
key_nums = []
pointer = 0
ans = ''
for i in key:
    if i in alpha1:
        key_nums += [alpha1.find(i)]
    elif i in alpha2:
        key_nums += [alpha2.find(i)]
for i in m:
    if i in alpha1:
        new_index = (alpha1.find(i) - key_nums[pointer]) % 26
        ans += alpha1[new_index]
        pointer = (pointer + 1) % len(key_nums)
    elif i in alpha2:
        new_index = (alpha2.find(i) - key_nums[pointer]) % 26
        ans += alpha2[new_index]
        pointer = (pointer + 1) % len(key_nums)
    else:
        ans += i
print(ans)
  • 得到0xGame{acb94092-e8bc-4963-88f6-4fcadbbfb6c7}

[Week 1] RSA-Baby

  • 写脚本
from Crypto.Util.number import *from hashlib import md5
def MD5(m):return md5(str(m).encode()).hexdigest()
Pub_Key = (547938466798424179, 80644065229241095)
Prv_Key = (547938466798424179, 488474228706714247)
Encrypt_msg = 344136655393256706
m = pow(Encrypt_msg,Prv_Key[1],Prv_Key[0])
flag = '0xGame{'+ MD5(m) +'}'
print(flag)

[Week 1] Number-Theory-CRT

  • hint提示CRT中国剩余定理和二次剩余

二次剩余： 二次剩余（Quadratic Residue）是数论中的一个概念。简单来说，如果一个整数 𝑥的平方模 𝑛结果等于某个整数 𝑎，那么这个 𝑎就称为模 𝑛的一个二次剩余。

  • 注意到 print(gmpy2.gcd(e,phi))的输出是2，也就是说令$e'=\frac{e}{2}$有$(m^\left. e'\right. )^2\equiv c\ mod\ n$
  • 要求解任意模数二次剩余先要 求解奇素数模数二次剩余 -具体理论查看此链
  • 据此推导过程编写脚本
from Crypto.Util.number import *
from hashlib import md5
import gmpy2
import sympy
from sympy.ntheory.modular import crt
def MD5(m):return md5(str(m).encode()).hexdigest()
Pub_Key = (1022053332886345327, 294200073186305890)
c = 107033510346108389
e = Pub_Key[1]
n = Pub_Key[0]
p = 970868179
q = 1052721013
phi = (p-1) * (q-1)
print(gmpy2.gcd(e,phi)) # 发现公约数2,分析得到二次剩余

def find_quadratic_residues(a, p):
    # 首先检查 a 是否是模 p 下的二次剩余
    if not sympy.is_quad_residue(a, p):
        return None  # 如果 a 不是二次剩余，返回 None
  
    # 使用 sympy 的 nthroot_mod 找到一个解
    x = sympy.nthroot_mod(a, 2, p, all_roots=False)
  
    # 计算另一个解
    second_solution = p - x
  
    return (x, second_solution)

x1 = find_quadratic_residues(c,p)       # 求解模p下的二次剩余
x2 = find_quadratic_residues(c,q)       # 求解模q下的二次剩余

for i in x1:
    for j in x2:
        remainders = [i,j]
        mods = [p,q]
        m_ = crt(mods, remainders)[0]   # CRT合并得到模n的二次剩余解
        c_ = m_%n

        e_ = e//2
        d = inverse(e_,phi)
        m = pow(c_,d,n)

        flag = '0xGame{'+ MD5(m) +'}'
        print(flag)
  • 注意的是，对于求解二次剩余有两解，所以在合并的时候都可以作为合并用的解
  • 所以遍历所有组合，得到正确flag
  • 0xGame{127016d0be858ef48a99723710ad4d49}

[Week 2] Diffie-Hellman

  • Diffie-Hellman题目是一个很好的hint，去了解了一下
  • 这是一种公钥交换的算法，在A，B两人处各自生成一对密钥（A，a）和（B，b）
  • 其中A和B是公钥用来互相间传输的，a和b是私钥，保存在本地
  • 然后两人用自己的私钥和对方的公钥就可以生成出S（共享公钥），两人计算出来的S是相同的
  • 然后查看题目附件，就是在靶机上生成（A，a），并发送A
  • 那本地为了能建立通信，同样也生成（B，b），并发送B。（此处生成过程可以套用附件的函数）
  • 此时靶机便会计算出S，继而计算出MD5，并以此用作AES加密的密钥
  • 最终输出密文
  • 那本地同样用b和A生成S，然后用自带库AES解密密文
  • 编写脚本
from string import ascii_letters, digits
from hashlib import sha256
from itertools import product
from Crypto.Cipher import AES
from hashlib import md5
from pwn import *

ip = '118.195.138.159' #要netcat的ip
port = 10000 #端口
io = remote(ip,port)

def proof():
	io.recvuntil(b'XXXX+')
	proof = io.recvuntil(b')')[:-1]
	io.recvuntil(b'== ')
	hash = io.recvuntil(b'\n')[:-1].decode()
	dict = ascii_letters + digits
	for word in product(dict, repeat=4):
		word = ''.join(word).encode()
		if sha256( (word+proof) ).hexdigest() == hash: break
	io.sendlineafter(b'XXXX: ',word)

def MD5(m):return md5( str(m).encode() ).digest()

proof()
q,g = io.recvline().decode()[15:-2].split(", ")
q,g = int(q),int(g)
Bob_PriKey = randint(1, q)
Bob_PubKey = pow(g, Bob_PriKey, q)
Alice_PubKey = int(io.recvline().decode()[15:-1])
print(f"Alice_PubKey={Alice_PubKey}")
io.recvuntil(b"[+] Give me the Bob_PubKey\n>")
io.sendline(str(Bob_PubKey).encode('utf-8'))
io.recvline()
c = io.recvline().decode()[17:-1]
Share_Key = pow(Alice_PubKey,Bob_PriKey,q)
Cipher = AES.new(MD5(Share_Key), AES.MODE_ECB)
m = Cipher.decrypt(bytes.fromhex(c))
print(m.strip(b"\x00"))
  • 0xGame{107c7960-d339-48b5-92b9-d59ad5644cf6}

[Week 2] Elgamal

  • 本题有关Elgamal数字签名
有关Elgamal数字签名

1. 系统初始化

选择一个大素数$p$和一个生成元$g$（通常是$g$是$p$的原根）。然后选择一个私钥$x$，满足 $1<x<p−1$。公钥由以下元素构成：

  • $p$
  • $g$
  • $y = g^xmod\ p$

2. 签名生成

要签署消息$m$，执行以下步骤：

  1. 哈希消息 ：使用安全的哈希函数（如SHA-256）计算消息的哈希值$H(m)$。
  2. 选择随机数 ：选择一个随机数$k$，满足$1<k<p−1$且$k$与$\varphi(p) = p-1$互质。
  3. 计算签名 ：
  • 计算$r = g^k mod\ p$。
  • 计算$s = k^{-1} \cdot (H(m) + x \cdot r) mod (p-1)$，其中$k^{-1}$是$k$模$\varphi(p)$的逆元。

签名为$(r,s)$。

3. 签名验证

接受放在接收到消息$m$和$(r,s)$后，可以通过以下步骤验证签名

  1. 验证$r$的有效性 ：检查$0<r<p$和$0<s<p−1$是否成立。
  2. 计算哈希值 ：计算$H(m)$
  3. 计算验证值 ：
  • 计算$u_1=y^rr^smod\ p$。
  • 计算$u_2=g^mmod\ p$。
  1. 验证签名 ：如果$u_1=u_2\ mod\ p$,则签名有效，否则无效。
  • 题干有明显提到在验签函数中参数校验出现问题
  • 检查发现，$(r,s)$是对$q$取模后的结果
  • 然而在验签中并没有校验$r$和$s$的大小，也就是说，我可以传入比$q$大的数
  • 这里就存在了伪造签名的可能性
  • 然而Elgamal并不是直接对明文加密，而是对其的sha256加密
  • 由于目前sha256的不可碰撞性，和无法预知性，并不能推测出伪造明文$m'$
  • 因而要依据$m$和$m'$的关系进行推算得到$r'$和$s'$
  • 以下为推导过程

$$ 根据验签原理，已知g^mmod\ p=y^rr^smod\ p $$

$$ 要构造(m',r',s')满足g^{m'}mod\ p=y^{r'}r'^{s'}mod\ p $$

$$ 存在关系m'=km\ mod(p-1) $$

$$ g^{m'}mod\ p=g^{km+k'(p-1)}mod\ p=(g^{km}mod\ p\cdot g^{k'(p-1)}mod\ p)mod\ p $$

$$ 根据费马小定理a^{\varphi (p)}mod\ p=1且gcd(p,1)=1 $$

$$ \Rightarrow g^{km}mod\ p=y^{kr}r^{ks}mod\ p $$

$$ \Rightarrow y^{kr+k_1(p-1)}(r+k_2p)^{ks}mod\ p=y^{r'}r'^{s'}mod\ p $$

$$ 使kr+k_1(p-1)=r+k_2p $$

$$ \Rightarrow k_1=(k-1)r\ mod\ p $$

$$ \therefore \left{\begin{matrix}r'=kr+k_1(p-1)\s'=ks\end{matrix}\right. $$

  • 然后手写脚本，逆元计算k
from string import ascii_letters, digits
from hashlib import sha256
from itertools import product
from Crypto.Util.number import *
from pwn import *

ip = '118.195.138.159' #要netcat的ip
port = 10002 #端口
io = remote(ip,port)

def proof():
	io.recvuntil(b'XXXX+')
	proof = io.recvuntil(b')')[:-1]
	io.recvuntil(b'== ')
	hash = io.recvuntil(b'\n')[:-1].decode()
	dict = ascii_letters + digits
	for word in product(dict, repeat=4):
		word = ''.join(word).encode()
		if sha256( (word+proof) ).hexdigest() == hash: break
	io.sendlineafter(b'XXXX: ',word)

proof()
q,g,y = io.recvline().decode()[23:-2].split(", ")
q,g,y = map(int,[q,g,y])
phi = q-1
msg = bytes.fromhex(io.recvline().decode()[16:-1])
r,s = io.recvline().decode()[28:-2].split(", ")
r,s = map(int,[r,s])
io.recvuntil(b"Now, it's your turn to help me sign something\n[+] Give me your message:\n>")

msg_ = (b'Welcome_to_0xGame2024').hex()
io.sendline(msg_.encode('utf-8'))
msg_ = bytes.fromhex(msg_)
m = int(sha256(msg).hexdigest(),16)
m_ = int(sha256(msg_).hexdigest(),16)
k = m_*inverse(m,(q-1))
s_ = k*s
k1 = (k-1)*r//q+(k-1)*r%q
k2 = (k-1)*r%q
r_ = r+k1*q

io.recvuntil(b"[+] Give me your r:\n>")
io.sendline(str(r_).encode('utf-8'))
io.recvuntil(b"[+] Give me your s:\n>")
io.sendline(str(s_).encode('utf-8'))
io.interactive()
  • 0xGame{93e9adb8-8a6d-4517-9c61-13081c413e41}

[Week 2] RC4

  • 分析代码发现，在util文件中定义了由密钥KEY生成密钥流keystream
  • 以及异或加密
  • 用脚本连接靶机通过人机验证
from string import ascii_letters, digits
from hashlib import sha256
from itertools import product
from pwn import *

ip = '118.195.138.159' #要netcat的ip
port = 10001 #端口
io = remote(ip,port)

def proof():
	io.recvuntil(b'XXXX+')
	proof = io.recvuntil(b')')[:-1]
	io.recvuntil(b'== ')
	hash = io.recvuntil(b'\n')[:-1].decode()
	dict = ascii_letters + digits
	for word in product(dict, repeat=4):
		word = ''.join(word).encode()
		if sha256( (word+proof) ).hexdigest() == hash: break
	io.sendlineafter(b'XXXX: ',word)

proof()
io.interactive()
  • 输入明文获取对应的密文，以及flag的密文
  • 注意：因为密钥流是256长度随机生成，所以输入明文必须比flag长，才能计算出加密时使用过的密钥
  • 编写脚本计算flag
m = "6162636465666768696a6b6c6d6e6f707172737475767778797a6162636465666768696a6b6c6d6e6f707172737475767778797a"
c = "1c2227967f1f7e60b38d47862cd1bf575075ac29b4108d2a7604e4368cc63b5f8d89d93701d6a26257f97da0952b15a5211d94d9"
enc = "4d380393771c6230ebd114d8728ce70a1730ec6cec5fcb313853e164d992730a8f87d3390cdffe6e59bc6aaf"
KEY = None
def recover_key(plaintext, ciphertext):
    pt_bytes = bytes.fromhex(plaintext)
    ct_bytes = bytes.fromhex(ciphertext)
    keystream = bytes([b1 ^ b2 for b1, b2 in zip(pt_bytes, ct_bytes)])
    return keystream
enc = bytes.fromhex(enc)
keystream = recover_key(m,c)
flag = bytes([b1 ^ b2 for b1, b2 in zip(enc, keystream)])
print(flag)
  • 此处的输入我用了[a-zA-Z]
  • 最终得到0xGame{81682337-6731-91c7-d060-3efcdfe1ba5f}

[Week 2] RSA-IV

  • 都是常见的RSA攻击类型，BUUCTF全刷到过，查看原理以及之前的wp
  • 主要不想手动解，便花了点时间用pwntool写了个自动脚本
  • challenge1是低加密指数攻击
  • challenge2是dp泄露
  • challenge3是维纳攻击
  • challenge4是共模攻击
from string import ascii_letters, digits
from hashlib import sha256
from itertools import product
from pwn import *
from Crypto.Util.number import *
from RSAwienerHacker import *
import gmpy2

ip = '118.195.138.159' #要netcat的ip
port = 10003 #端口
io = remote(ip,port)

def proof():
	io.recvuntil(b'XXXX+')
	proof = io.recvuntil(b')')[:-1]
	io.recvuntil(b'== ')
	hash = io.recvuntil(b'\n')[:-1].decode()
	dict = ascii_letters + digits
	for word in product(dict, repeat=4):
		word = ''.join(word).encode()
		if sha256( (word+proof) ).hexdigest() == hash: break
	io.sendlineafter(b'XXXX: ',word)

def slove0():
	io.recvuntil(b"[+] input choice:\n>")
	io.sendline(b'0')
	n,e,c = io.recvline().decode()[1:-2].split(', ')
	n,e,c = int(n),int(e),int(c)
	# 低加密指数广播攻击
	io.recvuntil(b">")
	while True:
		if gmpy2.iroot(c,e)[1]:
			m = gmpy2.iroot(c,e)[0]
			print(f"1:{m}")
			break
		c += n
	io.sendline(str(m).encode('utf-8'))

def slove1():
	io.recvuntil(b"[+] input choice:\n>")
	io.sendline(b'1')
	n,e,c,dp = io.recvline().decode()[1:-2].split(', ')
	n,e,c,dp = int(n),int(e),int(c),int(dp)
	# dp泄露
	a = dp*e-1
	for x in range(2,e):
		if a%x == 0:
			p = a//x+1
			if n%p == 0:
				q = n//p
				break
	d = inverse(e,(p-1)*(q-1))
	m = pow(c,d,n)
	print(f"2:{m}")
	io.sendline(str(m).encode('utf-8'))

def slove2():
	io.recvuntil(b"[+] input choice:\n>")
	io.sendline(b'2')
	n,e,c = io.recvline().decode()[1:-2].split(', ')
	n,e,c = int(n),int(e),int(c)
	# 维纳攻击
	d = hack_RSA(e,n)
	m = pow(c,d,n)
	print(f"3:{m}")
	io.sendline(str(m).encode('utf-8'))

def slove3():
	io.recvuntil(b"[+] input choice:\n>")
	io.sendline(b'3')
	n,e,c,e_,c_ = io.recvline().decode()[1:-2].split(', ')
	n,e1,c1,e2,c2 = int(n),int(e),int(c),int(e_),int(c_)
	# 共模攻击
	e1_e2=e1-e2
	s1 = inverse(e1_e2,e2)
	s2 = (1-e1*s1)//e2
	m = pow(c1,s1,n)*pow(c2,s2,n)%n
	print(f"4:{m}")
	io.sendline(str(m).encode('utf-8'))

proof()
slove0()
slove1()
slove2()
slove3()
io.interactive()
  • 最后拿到0xGame{2b5e024a-3c62-4f4a-afe0-b81851d9efc8}

[Week 2] LFSR-baby

  • LFSR是指线性(Linear)反馈(Feedback)移位(Shift)寄存器(Register)
  • 即有一个可移动的寄存器，通过反馈计算出下一个移动的数值，而其计算方式是线性的
  • 分析源码得到存在一个mask固定窗口和state滑动窗口，最初始的state即为seed
  • 两个列表中的二进制对应按位与运算，将所有结果异或保存至output
  • output即为生成的随机数，存入getrandbits函数中的result末尾
  • 将output存入state末尾，使窗口向后滑动一位
  • 继续反复操作，不断生成随机数
  • 注意到题目给的随机数是生成128位后的结果
  • 因此可以判断，一组随机数生成后正好完全将原先128位的seed从state变量中顶出

  • 如图，假设这是最后一次生成随机数，计算时的mask是1128，state是0127，上下同列的按位与运算，再异或，存入state的末尾（128）最终红色框内的128位数就是最终输出的随机数
  • 也就是说，可以通过脚本算出state中0位置是什么，然后再反复使用这种方式计算出原来完整的128位seed
  • 下面编写脚本
from hashlib import md5

def MD5(m):return md5(str(m).encode()).hexdigest()

def init_state(seed):
    result = [int(i) for i in bin(seed)[2:]]
    PadLenth = 128 - len(result)
    result += [ 0 ] * PadLenth
    assert len(result) == 128
    return result

def init_random(seed):
    result = [int(i) for i in bin(seed)[2:]]
    PadLenth = 128 - len(result)
    result = [ 0 ] * PadLenth + result
    assert len(result) == 128
    return result

random1 = 103763907686833223776774671653901476306
copy = random1
random2 = 136523407741230013545146835206624093442
Mask_seed = 245818399386224174743537177607796459213
random1,random2 = map(init_random,[random1,random2])
mask = init_state(Mask_seed)

def calc(state):
    for i in range(128):
        output = 0
        for i in range(1,128):
            output += state[i-1]*mask[i]
        output += state[-1]
        output = output%2
        state = [output] + state[:-1]
    return state
result = int(''.join(str(x) for x in calc(random2)),2) == copy
print(f"The calculation is {result}")
print("0xGame{"+MD5(int(''.join(str(x) for x in calc(random1)),2))+"}")
  • 代码中要注意随机数的长度并没有128位要手动补零，同时是在开头补，而不是调用源码的方法
  • 另外可以用第二个随机数来检验算法是否正确
  • 运行得到0xGame{030ec00de18ceb4ddea5f6612d28bf39}

[Week 2] LFSR-easy

  • 这题是依据种子和随机数倒推掩码
  • mask用$x_1~x_128$表示
  • seed用$s_1~s_128$表示
  • random用$x_129~x_256$表示
  • 可以得到如下的计算式

$$ \sum_{i=1}^{128} s_{i+n}x_i\ mod\ 2=s_{129+n}m\ ,\ n\in [0,128] $$

  • 因此可以写出在Zmod 2数域下的矩阵

$$ \begin{bmatrix} s_{1} & \dots & s_{128}\ \dots & \dots & \dots\ s_{128} & \dots & s_{255}\end{bmatrix}\begin{bmatrix} s_{129}\ \dots\ s_{256}\end{bmatrix} $$

  • 用Sage编写脚本计算解
from hashlib import md5

def MD5(m):return md5(str(m).encode()).hexdigest()

def init_state(seed):
    result = [int(i) for i in bin(seed)[2:]]
    PadLenth = 128 - len(result)
    result += [ 0 ] * PadLenth
    assert len(result) == 128
    return result

def init_random(seed):
    result = [int(i) for i in bin(seed)[2:]]
    PadLenth = 128 - len(result)
    result = [ 0 ] * PadLenth + result
    assert len(result) == 128
    return result

random1 = 299913606793279087601607783679841106505
random2 = 192457791072277356149547266972735354901
seed = 165943427582675380464843619836793254673
random1,random2 = map(init_random,[random1,random2])
seed = init_state(seed)

def solve_GF2_linear_system(A, b):
    """
    使用 SageMath 在 GF(2) 上求解线性方程组 Ax = b
    :param A: 系数矩阵
    :param b: 结果向量
    :return: 解向量 x
    """
    F = GF(2)
    A_GF2 = Matrix(F, A)
    b_GF2 = vector(F, b)

    try:
        x = A_GF2.solve_right(b_GF2)
        return x
    except ValueError:
        return None

def solution(m):
    a,b = m[0],m[1]
    solution = solve_GF2_linear_system(a, b)
    if solution:
        print(f"解向量为: {solution}")
        return solution
    else:
        print("无解")
        return None

def change(seed,random):
    All = seed + random
    a = [[0]*128 for _ in range(128)]
    b = random
    for i in range(128):
        a[i] = All[i:i+128]
    return (a,b)

ans1 = solution(change(seed,random1))
ans2 = solution(change(random1,random2))
print("The calculation is ",ans1 == ans2)
if ans1 == ans2:
    print("0xGame{"+MD5(int("".join(str(i) for i in ans1),2))+"}")
  • 解出0xGame{d56821feacab64cdb87c754ad06823a2}

[Week 3] ECC-DH

ECDH 算法的工作流程：

  1. 椭圆曲线选择 ：
  • 首先，双方需要选定一条公共的椭圆曲线。椭圆曲线可以用方程 $y^2 = x^3 + ax + b \mod p$表示，其中 $a$、$b$ 是曲线参数，$p$ 是素数，用于定义有限域上的曲线。
  • 在这条曲线上，双方还需要选定一个公共点 $G$，称为基点。基点是椭圆曲线上的一个已知点，通信双方将用它来生成密钥。
  1. 密钥生成 ：
  • Alice 随机生成一个私钥 $a$，这个私钥是一个整数。
    • 她计算对应的公钥 $A = a \cdot G$，这里的点乘是椭圆曲线点的标量乘法（多次加法运算）。
  • Bob 也生成一个随机的私钥 $b$，并计算出对应的公钥 $B = b \cdot G$。
  1. 公钥交换 ：
  • Alice 将她的公钥 $A$ 发送给 Bob，Bob 将他的公钥 $B$ 发送给 Alice。
  1. 共享密钥计算 ：
  • Alice 使用她的私钥 $a$ 和 Bob 的公钥 $B$ 计算共享密钥： $S = a \cdot B = a \cdot (b \cdot G) = (a \cdot b) \cdot G$
  • Bob 使用他的私钥 $b$ 和 Alice 的公钥 $A$ 计算共享密钥： $S = b \cdot A = b \cdot (a \cdot G) = (b \cdot a) \cdot G$
  • 由于点乘是交换的，Alice 和 Bob 最终计算得到相同的共享密钥 $S$。
  • 很好理解啊，不涉及比较难的数学知识，只要搞懂原理就行，也用会算
  • 和**[Week 2] Diffie-Hellman**逻辑上几乎一样，就是本地生成私钥和公钥，然后与靶机交互确定共享公钥
  • 最终用AES对称加密来传输数据
  • 上代码
from hashlib import md5, sha256
from itertools import product
from string import ascii_letters, digits
from Crypto.Cipher import AES
from pwn import *
from Util import *

addr = "nc 118.195.138.159 10004".split(" ")
io = remote(addr[1],int(addr[2]))

def MD5(m):return md5( str(m).encode() ).digest()

def proof():
	io.recvuntil(b'XXXX+')
	proof = io.recvuntil(b')')[:-1]
	io.recvuntil(b'== ')
	hash = io.recvuntil(b'\n')[:-1].decode()
	dict = ascii_letters + digits
	for word in product(dict, repeat=4):
		word = ''.join(word).encode()
		if sha256( (word+proof) ).hexdigest() == hash: break
	io.sendlineafter(b'XXXX: ',word)

proof()

a = 10809567548006703521
b = 9981694937346749887
p = 25321837821840919771
E = Curve(a, b, p)
g_x,g_y = map(int,io.recvline().decode()[15:-2].split(","))
a_x,a_y = map(int,io.recvline().decode()[20:-2].split(","))
G = Point(g_x,g_y,E)
A = Point(a_x,a_y,E)
b = randint(1, p)
B = b * G
io.sendlineafter(b"[+] Give me the Bob_PubKey.x\n>",str(B.x).encode('utf-8'))
Share_Key = b * A
Cipher = AES.new(MD5(Share_Key.x), AES.MODE_ECB)
io.recvline()
c = bytes.fromhex(io.recvline().decode()[21:-1])
m = Cipher.decrypt(c)
print(m)
io.interactive()
  • 0xGame{71234da9-baf8-406e-9cc7-d08ceedea945}

[Week 3] ECC-baby

  • ECC加密用来交换对称密钥
  • 可以发现素数p不是太大，于是尝试暴力计算key或k
  • 实测k和key都能爆出来
  • Sage脚本：Baby-step Giant-step 算法求解 ECDLP
# Sage 环境
def baby_step_giant_step(E, G, P, n):
    """
    Baby-step Giant-step 算法求解椭圆曲线离散对数问题
    E: 椭圆曲线
    G: 基点
    P: 已知点 P = k * G
    n: 椭圆曲线的阶
    """
    m = ceil(sqrt(n))
  
    # Step 1: Baby-step, 计算表 {i: i*G} for i = 0, 1, ..., m-1
    baby_steps = {}
    for i in range(m):
        baby_steps[i * G] = i
  
    # Step 2: Giant-step, 计算 j * (-m * G)
    inv_mG = -m * G
    current = P
  
    for j in range(m):
        if current in baby_steps:
            return j * m + baby_steps[current]
        current += inv_mG
  
    # 如果没有找到解，返回None
    return None


# 椭圆曲线参数
p = 4559252311 # 椭圆曲线的素数域
a = 1750153947 # 椭圆曲线参数 a
b = 3464736227 # 椭圆曲线参数 b
E = EllipticCurve(GF(p), [a, b]) # 定义椭圆曲线

# 基点 G 和已知点 P = k * G
G = E(2909007728, 1842489211)
P = E(1923527223,2181389961)

# 椭圆曲线的阶
n = E.order()

# 使用 Baby-step Giant-step 求解 k
key = baby_step_giant_step(E, G, P, n)
if k is not None:
    print(f"Found key: {key}")
else:
    print("No solution found.")
  • 得到 key = 1670419487
  • 然后用内置的点乘计算$P = G' \cdot key$
  • 再进行逆运算$M = C + ( - P')$
  • 又可以根据定义可以知道$−Q=(x_Q,−y_Qmod\ p)$
  • 所以搓脚本
from hashlib import md5
from Crypto.Cipher import AES
from Util import *

def MD5(m):return md5(str(m).encode()).digest()

p = 4559252311
a = 1750153947
b = 3464736227
curve = Curve(a, b, p)
G = Point(2909007728,1842489211,curve)
P = Point(1923527223,2181389961,curve)
G_= Point(1349689070,1217312018,curve)
C = Point( 662346568,2640798701,curve)
enc= bytes.fromhex("29bb47e013bd91760b9750f90630d8ef82130596d56121dc101c631dd5d88201a41eb3baa5aa958a6cd082298fc18418")
key = 1670419487
P_ = G_*key
M = C + Point(P_.x,(-P_.y)%p,curve)
Cipher = AES.new(MD5(M.x), AES.MODE_ECB)
m = Cipher.decrypt(enc)
print(m)
  • 0xGame{0b0e28c2-b36d-d745-c0be-fcf0986f316a}

[Week 3] EzLogin-I

  • 分析源码，要使输入的cookie能被正确解析为{"username": "admin", "time": ……}才能得到flag
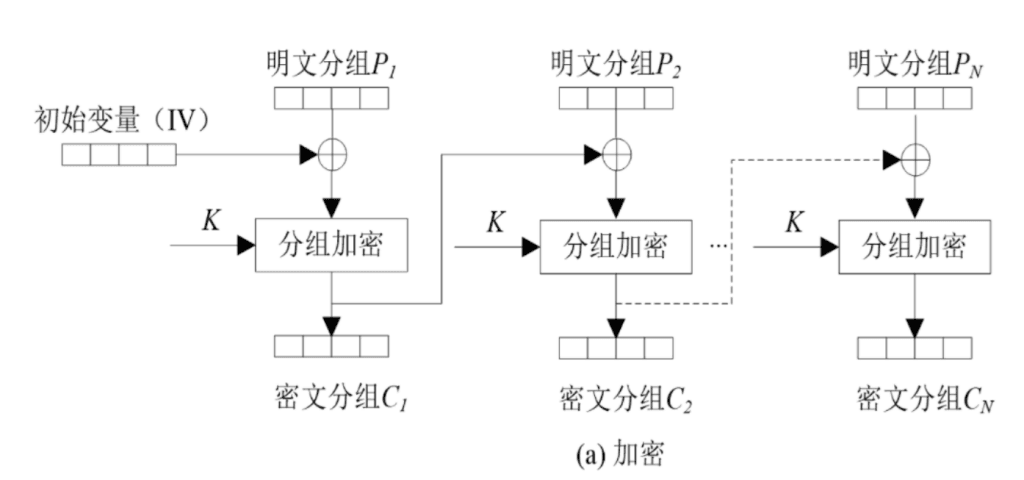
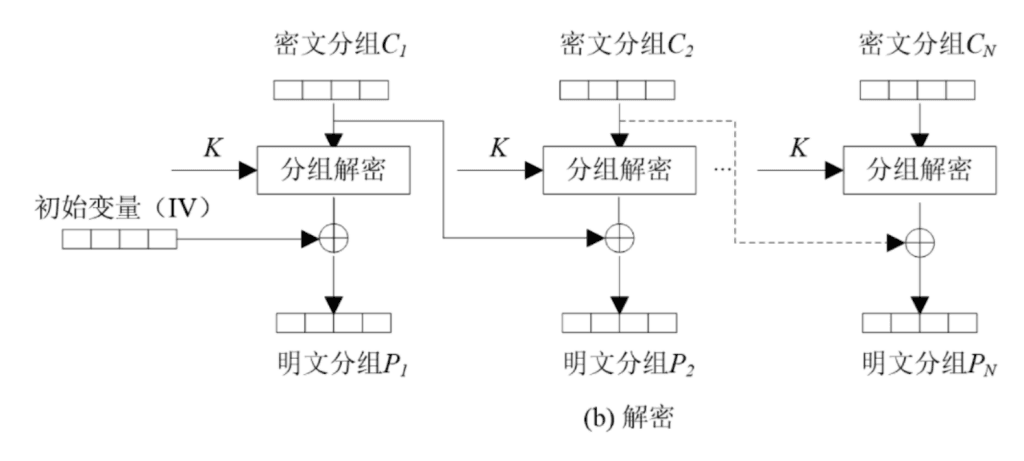
  • 分析发现对输入转化为json然后进行了AES.CBC加密，再以Base64输出
  • 可以利用CBC加密特性，字节翻转攻击，定向改变某个解析后的明文
  • 下面引用CBC加密和解密的图示

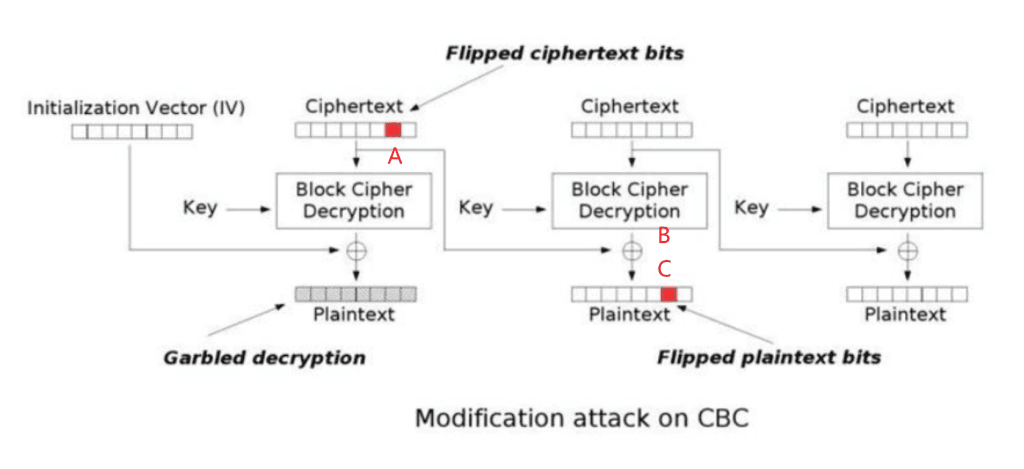
  • 下面是反转攻击示例

  • 由于C=B⊕A，可以特定改变A，使C变成想要的指定字符C'
  • 推导得A’=A⊕C⊕C'
  • 但要注意的是，虽然C被指定改变，但A的改变会影响到整段第一明文的变化
  • 而json是格式固定的，也就意味着只能修改通过修改IV来修改第一明文，而无法改变第二明文
  • 构造payload
from base64 import b64decode, b64encode
from pwn import *


addr = "nc 118.195.138.159 10005".split(" ")
io = remote(addr[1],int(addr[2]))

io.sendlineafter('''+--------------+
| [R] Regist   |
| [L] Login    |
| [F] Getflag  |
+--------------+

[+] Tell me your choice:
>''',b"R")
io.sendlineafter("[+] username:\n>",b"zdmin")
base64en = io.recvline().decode()[13:]
base64de = bytearray(b64decode(base64en))
base64de[14] = base64de[14] ^ ord("z") ^ ord("a")
fake_cookie = b64encode(bytes(base64de))
io.sendlineafter("[+] Tell me your choice:\n>",b"L")
io.sendlineafter("[+] cookie:\n>",fake_cookie)
io.interactive()
  • 0xGame{ad34acff-a813-4bc3-a44a-c270edf244b7}

[Week 3] EzLogin-II

  • 在CBC加密的基础上，由于是分块处理，所以要对不能成块的部分进行填充
  • 这里填充通常采用的是PKCS#7的标准进行填充，即填充字符个数与填充值相同，并且必须填充
  • 如1234→1234\0x04\0x04\0x04\0x04
  • 或12345678→12345678\0x08\0x08\0x08\0x08\0x08\0x08\0x08\0x08
  • (上述是对于8个字节分块的情况举例)

  • 下面讲述Padding Oracle Attack（或者CTF Wiki会比我更详细）
  • 参考上一题的解密方式能发现
  • 由于Block i在经过key解密后要和Block i-1异或得到Plaintxt
  • 也就是说可以改变Block i-1的值来改变Plaintxt的结果，这都是上一题已知的
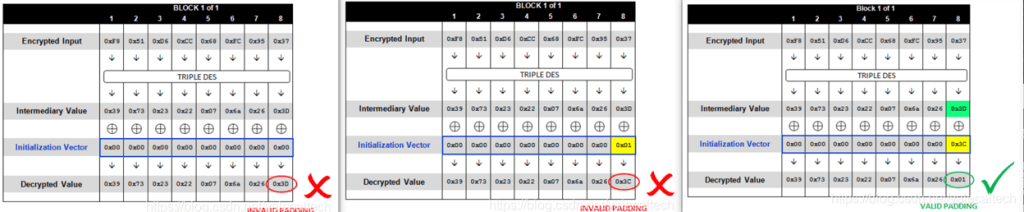
  • 这题由于对明文脱padding的方法unpad中有Unpad error的报错
  • 可以通过构造Block i-1的最后一个字节使得Plaintxt中的最后一个字节为\0x01
  • 可以发现这样是不会报错的，而其他不正确的填充则会报错
  • 所以可以通过靶机的回显来判断构造是否正确，从而得到正确明文（已知假明文，假IV可以推出中间值，与真IV异或后得到真明文）
  • 然后再对倒数第二个字节同样方式爆破
  • 注意：这里要保证爆破字节以外的字节满足假明文为\0x02
  • 明白原理后就可以手搓脚本了
from base64 import b64decode, b64encode
from pwn import *

addr = "nc 118.195.138.159 10005".split(" ")
io = remote(addr[1], int(addr[2]))

io.sendlineafter('''+--------------+
| [R] Regist   |
| [L] Login    |
| [F] Getflag  |
+--------------+

[+] Tell me your choice:
>''', b"F")
base = io.recvline().decode()[20:]
enc = b64decode(base)
io.sendlineafter("[+] Tell me your choice:\n>", b"L")

alpha = [4]

for i in "0123456789abcdef-}{xGame":
    alpha += [ord(i)]

def padding_oracle_attack(ciphertext):
    # 分块
    blocks = [ciphertext[i:i + 16] for i in range(0, len(ciphertext), 16)]
    decrypt = []
    for block_index in range(1,len(blocks))[::-1]:
        # 构造IV和密文块
        current_block = blocks[block_index]
        iv = blocks[block_index-1]
        fake_iv = bytearray(iv)
        # 遍历IV块
        for attack_index in range(1,17):
            # 伪造IV块中先前值
            for change_index in range(1,attack_index):
                fake_iv[-change_index] = fake_iv[-change_index] ^ (attack_index-1) ^ attack_index
            # 遍历字节值
            for bytes_value in range(1,256):
                fake_iv[-attack_index] = bytes_value
                print(f"尝试: bytes_value: {bytes_value:3}, fake_iv: {fake_iv.hex()}")
                print(f"已得: {decrypt}\n")
                if sendtest(fake_iv + current_block):
                    if (attack_index ^ bytes_value ^ iv[-attack_index]) in alpha:
                        decrypt += [attack_index ^ bytes_value ^ iv[-attack_index]]
                        break
    return "".join([chr(i) for i in decrypt])

def sendtest(modified_ciphertext):
    # 测试靶机响应
    encoded_ciphertext = b64encode(modified_ciphertext).decode()
    io.sendlineafter("[+] cookie:\n>", encoded_ciphertext)
    resp = io.recvline().decode()
    print("响应:", resp[:-1])
    return resp != "[!] Unkown Wrong\n"

# 执行 padding oracle 攻击
decrypted = padding_oracle_attack(enc)[::-1]
print("解密结果: ", decrypted)
io.close()

注意几个点

  1. 原码在经过unpad之后有decode的处理，所以说不能转化为字符的字节同样会引发Unkown Wrong的报错，所以构造IV的时候不要用随机值或者全0填充
  2. 由于直接认定flag是uuid格式并且是由\0x04填充的，所以可以写入alpha，来避免其他同样可能满足不报错的可能性。（正常来说对于末尾字节会有多种可能，若当前可能无法继续往下爆破的时候，需要代码处理好回退操作。）
  3. 靶机测试响应中，有可能会成功json load从而触发TypeError Wrong报错，因此直接判断是否为Unkown Wrong即可
  • 0xGame{6e02937e-634d-4f6f-8ef6-e5f387006cde}

大佬的解法

速度很快，用了明文攻击，来自三顺七

from pwn import *
from base64 import b64encode, b64decode
from time import time
#context(log_level = 'debug')

s = time()
xor = lambda a, b: bytes([x^y for x, y in zip(a, b)])

io = remote('118.195.138.159', 10005)

io.sendlineafter(b'>', b'R')
io.sendlineafter(b'>', b'Admin')
io.recvuntil(b'[+] cookie : ')
cookie = io.recvline()[:-1]

prefix = b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x20\x00'
cookie = xor(b64decode(cookie), prefix) + b64decode(cookie)[16:]
io.sendlineafter(b'>', b'L')
io.sendlineafter(b'>', b64encode(cookie))
print(io.recvline().decode())


def Send(payload):
	io.sendlineafter(b'>', b64encode(payload))
	result = io.recvline()
	#print(result)
	if result == b'[!] Unkown Wrong\n':
		return 0
	elif result == b'[!] JSON Wrong\n':
		return 1
	elif result == b'[!] TypeError Wrong\n':
		return 1

def PaddingOracle(before,after):
	d_iv = [0 for _ in range(16)]
	dict = list(b'0123456789abcdef{}xGame-') + [i for i in range(2, 16)]
	print(f'dict = {dict}')
	for i in range(1, 17):
		flag = 1
		Pad = [0 for _ in range(17-i)]
		if i == 1:
			Index = []
		else:
			Index = [i for _ in range(i-1)]
		Prefix = Pad + Index

		for j in dict:
			d_iv[-i] = j ^ i
			IV = bytes(xor(xor(before,d_iv), Prefix))
			payload = IV + after
			result = Send(payload)

			if result == 1:
				d_iv[-i] = j
				flag = 0
				print(i, d_iv)
				break

		if flag == 1:
			for j in dict[::-1]:
				d_iv[-(i-1)] = j ^ i
				IV = bytes(xor(xor(before,d_iv), Prefix))
				payload = IV + after
				result = Send(payload)

				if result == 1:
					d_iv[-(i-1)] = j
					print(i, d_iv)
					break

			for j in dict:
				d_iv[-i] = j ^ i
				IV = bytes(xor(xor(before,d_iv), Prefix))
				payload = IV + after
				result = Send(payload)

				if result == 1:
					d_iv[-i] = j
					flag = 0
					print(i, d_iv)
					break

	return bytes(d_iv)

def Oracle():
	io.sendlineafter(b'>', b'F')
	io.recvuntil(b'[+] Here is flag2 : ')
	enc = io.recvline()
	print(enc)
	msg = b64decode(enc)
	io.sendlineafter(b'>', b'L')
	result = b''
	BlockLength = len(msg)//16
	print(f'[+] BlockLength = {BlockLength}')
	Block = [msg[16 * i: 16 * (i+1)] for i in range(BlockLength)]
	for i in range(0,BlockLength - 1):
		print(f'[x] Procing BlockIndex : {i}')
		result += PaddingOracle(Block[i], Block[i+1])
	return result

flag2 = Oracle()
print(flag2)
io.close()
e = time()
print(f'[+] Cost : {e-s}')

[Week 3] LLL-I

关于格的一些大佬讲解-链接-链接

  • 原理比较难搞（我不会
  • 题干说LLL算法出来就行，所以写如下sage
from sage.all import *

B = Matrix(ZZ, [[1849784703482951012865152264025674575, 2664848085955925754350117767673627932, 2099783527396520151610274180590854166, 1020558595577301617108111920545804527],
                   [1207449566811121614020334020195802372, 1954621976999112878661150903673543232, 1326050406731534201574943690688237338, 1361813208094227445768111591959011963],
                   [888810907577479776819993141014777624 , 1216302736807928240875874427765340645, 1027359437421599069599327712873719567, 238961447144792739830554790892164336 ],
                   [60622164517940943037274386912282     , 82958508138755168576836012717468     , 70072118066826856564329627650828     , 16296740862142507745322242235326     ]])
print(B.LLL())
  • 由于flag混入在第一行，得到矩阵后取第一行，无视正负就是flag
  • （由于LLL算出来的是最短基向量，而正负不会影响最短的特性）
  • 脚本
from Crypto.Util.number import *
c = [ -58596440058654765094286903,  -69377248846131264731819316,  -60910008503494441471652194,  -58497746791226042414948989]
print("".join([(long_to_bytes(abs(i))).decode() for i in c]))
  • 0xGame{04679c42-2bc1-42b2-b836-1b0ca542f36b}

后续补充的原理

  • $CM=S$由于$||M||=1$可以认为$C$与$S$是等价的
  • 而又由于$C$是随机生成的其施密特正交化程度几乎可以认为是 最高 -随机矩阵正交性的证明
  • 因此对$S$进行LLL算法求其等价正交格基就等于求$C$

[Week 3] LLL-II

参考HNP讲解

  • 基于LCG的生成规律$X_{n+1}=aX_n+b\ mod\ m$
  • 已知如下式子

$$ \left{\begin{align} Cs[0]&=aseed\ mod\ m\ Cs[1]&=aCs[0]+b_1\ mod\ m\ Cs[i]&=aCs[i-1]+b_i\ mod\ m\ b_i&=Cs[i]-aCs[i-1]+k_i*m\ \end{align}\right. $$

  • 然后构造格

$$ \begin{array}
(k_1&k_2&k_3&k_4&-a&1) \left[\matrix{ m&0&0&0&0&0\ 0&m&0&0&0&0\ 0&0&m&0&0&0\ 0&0&0&m&0&0\ Cs[0]&Cs[1]&Cs[2]&Cs[3]&K/n&0\ Cs[1]&Cs[2]&Cs[3]&Cs[4]&0&K

} \right] = (b_1&b_2&b_3&b_4&K\cdot a/m&K) \end{array} $$

  • 其中$K$是$b_i$的估计值令$K=2^{128}$
  • 然后就可以根据构造的格，来用sage求解
from Crypto.Util.number import *

cs = [
    11804527453299586684489593808016317337345238230165321056832279785591503368758306671170625597063579251464905729051049524014502008954170088604924368057540940, 4930922884306486570759661288602557428608315558804950537470100263019228888817481617065454705843164809506859574053884206133344549895853064735361336486560981, 5380263856446165449531647111260010594620416730932539097782399557603420658350407080366132490174060420530708293564252852668431923560882648691392446521188465, 10746696290782998433216934286282230556131938525513632178308443345441147075710552571129957873399395862207656161609046567289600084193860244770966610161184627, 2195032957511830992558961021566904850278796737316238566513837995297394215638259916944087623923636789312134734949452839561765171446217520081402769962517110]
m = 12813864523019740432913161815051292412705285817864701047922722497269479288096574264414061282833203433542813637861620032851255308640850882149603687035724753

M = matrix(QQ,6,6)
for i in range(4):
    M[i,i] = m
    M[-2,i] = cs[i]
    M[-1,i] = cs[i+1]
k=2^254
M[-2,-2]=k/m
M[-1,-1]=k
L=M.LLL()
print(L[0])
print(L[1])
print(L[2])
print(L[3])
print(L[4])
print(L[5])
res=L[1][-2].numerator()/k
a=abs(res)
print(a)
# 不知道为什么下面代码Sage中运行不了，但单独拎出来是可以运行的
from hashlib import md5
def MD5(m):return md5(str(m).encode()).hexdigest()
seed=cs[0]*inverse(a,m)%m
flag = '0xGame{' + MD5(seed) + '}'
print(flag)
  • 0xGame{2db84757dd4197f9b9441be25f35bfd5}

[Week 3] LLL-III

  • 没搞懂LLL但找到了板子
  • 几乎一样，改改数据和移位
from Crypto.Cipher import AES
from Crypto.Util.number import *
from hashlib import md5

def MD5(m):return md5(str(m).encode()).hexdigest()

m = 181261975027495237253637490821967974838107429001673555664278471721008386281743
a = 80470362380817459255864867107210711412685230469402969278321951982944620399953
b = 108319759370236783814626433000766721111334570586873607708322790512240104190351
c = [2466192191260213775762623965067957944241015, 1889892785439654571742121335995798632991977, 1996504406563642240453971359031130059982231, 1368301121255830077201589128570528735229741, 3999315855035985269059282518365581428161659, 3490328920889554119780944952082309497051942, 2702734706305439681672702336041879391921064, 2326204581109089646336478471073693577206507, 3428994964289708222751294105726231092393919, 1323508022833004639996954642684521266184999, 2208533770063829989401955757064784165178629, 1477750588164311737782430929424416735436445, 973459098712495505430270020597437829126313, 1849038140302190287389664531813595944725351, 1172797063262026799163573955315738964605214, 1754102136634863587048191504998276360927339, 113488301052880487370840486361933702579704, 2862768938858887304461616362462448055940670, 3625957906056311712594439963134739423933712, 3922085695888226389856345959634471608310638]

h = [0] + c

length = len(h)
for i in range(length):
    h[i] <<= 115

A = [1]
B = [0]

for i in range(1, len(h)-1):
	A.append(a*A[i-1] % m)
	B.append((a*B[i-1]+a*h[i]+b-h[i+1]) % m)

A = A[1:]
B = B[1:]

Ge = Matrix(ZZ,length,length)

for i in range(len(A)):
    Ge[i,i] = m
    Ge[-2,i] = A[i]
    Ge[-1,i] = B[i]

K = 2**115
Ge[-2,-2] = 1
Ge[-1,-1] = K

for line in Ge.LLL():
    if abs(line[-1]) == K:
        L1 = line[-2]
        seed1 = h[1] + L1
        seed = (seed1 - b) * inverse(a,m) % m
        print(f"seed = {seed}")
        print('0xGame{' + MD5(seed) + '}')
  • 0xGame{459049e068d93f6d70f1ea0da705264a}

[Week 4] SIDH

  • SIDH后量子安全密钥交换协议，嗐（学不懂
  • 但是
  • DH，说的很明白了，就是密钥交换
  • 看源码发现只要模仿靶机生成密钥然后和靶机进行交互就可以了
  • 实测：9.3版本代码无法正常运行，建议用10.4
  • 抄靶机代码
from pwn import *

ea, eb = 110, 67
p = 2**ea * 3**eb - 1
F.<i> = GF(p**2, modulus=[1,0,1])

E0 = EllipticCurve(F, [1,0])

addr = "nc 118.195.138.159 10009".split(" ")

io = remote(addr[1],int(addr[2]))
recv = io.recvline().decode()[10:-2]
RA_ = re.split(r"\*i \+ |,", recv)
RA = E0(int(RA_[0])*i + int(RA_[1]), int(RA_[2])*i + int(RA_[3]))
print(f"RA={RA.xy()}")

PB = E0.random_point()
QB = E0.random_point()
sB = randint(0, 2**ea)
RB = PB + sB * QB
xy = [str(i).split("*i + ") for i in RB.xy()]
payload1 = ",".join(",".join(i) for i in xy)
print(f"RB={RB.xy()}")
print(f"payload1={payload1}")

phi_A = E0.isogeny(RA, algorithm='factored')
E_A = phi_A.codomain()

R_share = phi_A(PB) + sB * phi_A(QB)
phi_share = E_A.isogeny(R_share, algorithm='factored')
secret = phi_share.codomain().j_invariant()
payload2 = ",".join(i for i in str(secret).split("*i + "))
print(f"secret={secret}")
print(f"payload2={payload2}")

io.sendlineafter("[+] Give me RB:\n>",payload1.encode())
io.sendlineafter("[+] Tell me the secret\n>",payload2.encode())
flag = io.recvline()
print(flag)

io.interactive()
  • 可能要多跑几次，因为secret出现整数的可能性还是挺大的（不知道为什么
  • 0xGame{4179c8c3-db69-4fb0-bd14-ef6c76ddb973}

[Week 4] RNG

  • 这是一个32位的MT19937伪随机数生成器
  • 真实原理没怎么搞懂还是移步Cryptography wiki吧，那里比较详细
  • 源码分析主要是三个操作，一个是在类生成时候的init初始化
  • 二是624一组过后的twist旋转，在生成第一个数之前也经过旋转
  • 三是每次生成随机数的函数extract
  • 第一步逆向可以看Cryptography wiki，后两步逆向我参考的是独奏の小屋
  • 套模板
from pwn import *
import random
from sympy import invert

addr = "nc 118.195.138.159 10006".split(" ")
io = remote(addr[1],int(addr[2]))
io.recvline()
result = [int(i) for i in io.recvline().decode()[1:-2].split(", ")]

# 逆向MT19937
class MT19937Recover:
    def unshiftRight(self, x, shift):
        res = x
        for i in range(32):
            res = x ^ res >> shift
        return res

    def unshiftLeft(self, x, shift, mask):
        res = x
        for i in range(32):
            res = x ^ (res << shift & mask)
        return res

    def untemper(self, v):
        v = self.unshiftRight(v, 18)
        v = self.unshiftLeft(v, 15, 0xefc60000)
        v = self.unshiftLeft(v, 7, 0x9d2c5680)
        v = self.unshiftRight(v, 11)
        return v

    def go(self, outputs, forward=True):
        result_state = None

        assert len(outputs) >= 624

        ivals = []
        for i in range(624):
            ivals.append(self.untemper(outputs[i]))

        if len(outputs) >= 625:
            challenge = outputs[624]
            for i in range(1, 626):
                state = (3, tuple(ivals+[i]), None)
                r = random.Random()
                r.setstate(state)

                if challenge == r.getrandbits(32):
                    result_state = state
                    break
        else:
            result_state = (3, tuple(ivals+[624]), None)

        rand = random.Random()
        rand.setstate(result_state)

        if forward:
            for i in range(624, len(outputs)):
                assert rand.getrandbits(32) == outputs[i]

        return ivals

# 逆向twist
def untwist(newState, flag: bool = True):
    oldState = [0] * 624
    for i in range(624 - 1, -2, -1):
        x = newState[i] ^ newState[(i + 397) % 624]
        if x & 0x80000000 == 0x80000000:
            x ^= 0x9908b0df
            x <<= 1
            x |= 1
        else:
            x <<= 1
        if i > -1:
            oldState[i] |= x & 0x80000000
        if i + 1 < 624:
            oldState[i + 1] |= x & 0x7fffffff
        if i == 227 and flag:
            newState = list(newState[:227]) + oldState[227:]
    return oldState

# 逆向__init__
def _int32(x):
    return int(0xFFFFFFFF & x)

def invert_right(res,shift):
    tmp = res
    for i in range(32//shift):
        res = tmp^res>>shift
    return _int32(res)

def recover(last):
    n = 1<<32
    inv = invert(1812433253,n)
    for i in range(623,0,-1):
        last = ((last-i)*inv)%n
        last = invert_right(last,30)
    return last

mtc = MT19937Recover()
newstate = mtc.go(result)
oldstate = untwist(newstate)
seed = recover(oldstate[-1])
print(f"seed={seed}")

io.sendlineafter("[+] seed = ?\n>",str(seed).encode())
io.interactive()
  • 0xGame{2569bd55-a14d-46d8-81f5-e1397e4be7bc}
  • p.s. extract逆向还是比较好理解（博客讲的很清楚），其他两种操作就难理解了

[Week 4] Coppersmith-I

  • 这是RSA已知p高位攻击Factoring with High Bits Known
  • 所以可以构造出p用sage求解小根
  • 参考博客
n = 135500646574582511239845764710311769260801998982429500680171919823431178899526463566215834234383331374445093363969218810906991784569340270510936759183504496584225937614940086329775325893307453919055830270986601152002191368431527285285313669979358099782497422114870417519470053198217401297960844455029559146309
c = 41763956818640145556632229720626372656921875856507389014855753965024986594502113237270745517422792354256348958542864591249410500750410658988509136242435502259172258432676502846729088278202750721760451160668653746019965695721844819587671602925551448624324524027931677927410810126647175483982178300855471710099
e = 65537
p_high = 918578024558168836638919636090777586135497638818209533615420650282292168631485

for i in range(2**5):
    p4 = p_high << 5			#这里需要先爆破5位，使得知道264位以后再恢复p
    p4 = p4 + i
    kbits = 248
    p4 = p4 << kbits
    R.<x> = PolynomialRing(Zmod(n))
    f = x + p4
    res = f.small_roots(X=2^kbits, beta=0.4, epsilon=0.01)
    if res != []:
        p = p4 + res[0]
        print(p)
        break
  • 得到p之后常规解密文就行
  • 0xGame{8f4c17cb-442a-49bd-830a-d16af225a5c5}