CS229 Lecture notes
| 原作者 | 翻译 | 校对 |
|---|---|---|
| Andrew Ng 吴恩达,Kian Katanforoosh | CycleUser | XiaoDong_Wang |
| 相关链接 |
|---|
| Github 地址 |
| 知乎专栏 |
| 斯坦福大学 CS229 课程网站 |
| 网易公开课中文字幕视频 |
现在开始学深度学习。在这部分讲义中,我们要简单介绍神经网络,讨论一下向量化以及利用反向传播(backpropagation)来训练神经网络。
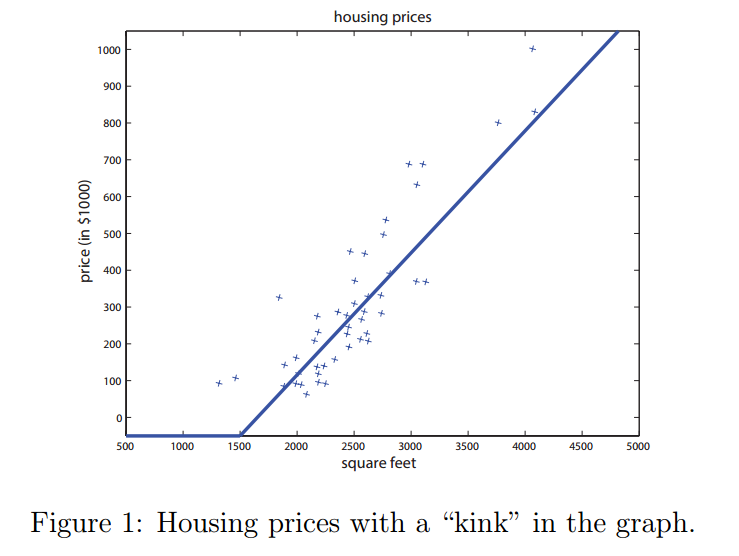
我们将慢慢的从一个小问题开始一步一步的构建一个神经网络。回忆一下本课程最开始的时就见到的那个房价预测问题:给定房屋的面积,我们要预测其价格。
在之前的章节中,我们学到的方法是在数据图像中拟合一条直线。现在咱们不再拟合直线了,而是通过设置绝对最低价格为零来避免有负值房价出现。这就在图中让直线拐了个弯,如图1所示。
我们的目标是输入某些特征$x$到一个函数$f(x)$中,然后输出房子$y$的价格。规范来表述就是:$f:x\rightarrow y$。可能最简单的神经网络就是定义一个单个神经元(neuron)的函数$f(x)$,使其满足$f(x)=\max(ax+b,0)$,其中的$a,b$是参数(coefficients)。这个$f(x)$所做的就是返回一个单值:要么是$(ax+b)$,要么是$0$,就看哪个更大。在神经网络的领域,这个函数叫做一个ReLU(英文读作'ray-lu'),或者叫整流线性单元(rectified linear unit)。更复杂的神经网络可能会使用上面描述的单个神经元然后堆栈(stack)起来,这样一个神经元的输出就是另一个神经元的输入,这就得到了一个更复杂的函数。
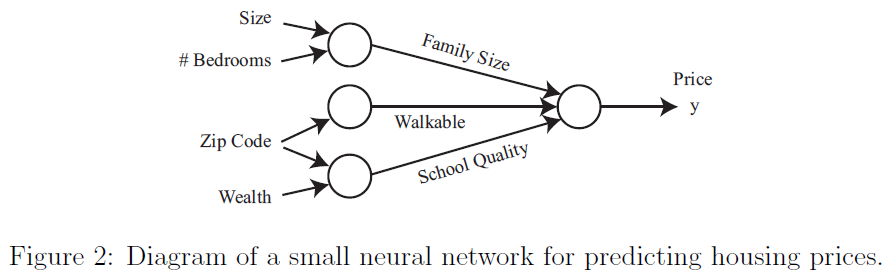
现在继续深入房价预测的例子。除了房子面积外,假如现在你还知道了卧房数目,邮政编码,以及邻居的财富状况。构建神经网络的过程和乐高积木(Lego bricks)差不多:把零散的砖块堆起来构建复杂结构而已。同样也适用于神经网络:选择独立的神经元并且堆积起来创建更复杂的神经元网络。
有了上面提到的这些特征(面积,卧房数,邮编,社区财富状况),就可以决定这个房子的价格是否和其所能承担的最大家庭规模有关。假如家庭规模是房屋面积和卧室数目的一个函数(如图2所示)。邮编(zip code)则可以提供关于邻居走动程度之类的附加信息(比如你能走着去杂货店或者去哪里都需要开车)。结合邮编和邻居的财富状况就可以预测当地小学的教育质量。给了上面这三个推出来的特征(家庭规模,交通便利程度,学校教育质量),就可以依据这三个特征来最终推断房价了。
我们就已经描述了上面这个神经网络了,就如同读者应该已经理解了确定这三个因素来最终影响房屋。神经网络的一个神奇之处就在于你只需要有输入特征向量$x$以及输出$y$,而其他的具体过程都交给神经网络自己来完成。用神经网络学习中介特征(intermediate features)的这个过程叫做端到端学习(end-to-end learning)。
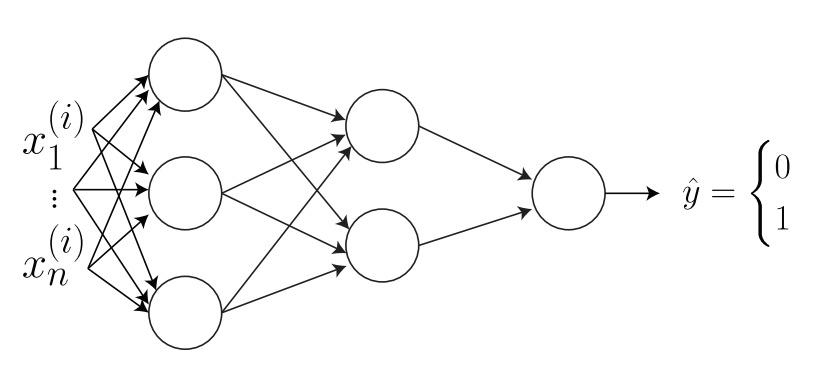
参考上面关于房价的例子,严格来说,输入到神经网络的是一个输入特征的集合$x_1,x_2,x_3,x_4$。我们将这四个特征连接到三个神经元(neurons)。这三个“内部(internal)”神经元叫做隐藏单元(hidden units)。这个神经网络的目标是要去自动判定三个相关变量来借助着三个变量来预测房屋价格。我们只需要给神经网络提供充足数量的训练样本$(x^{(i)},y^{(i)})$。很多时候,神经网络能够发现对预测输出很有用的一些复杂特征,但这些特征对于人类来说可能不好理解,因为可能不具备通常人类所理解的常规含义。因此有人就把神经网络看作是一个黑箱(black box,意思大概就是说内部过程不透明),因为神经网络内部发掘的特征可能是难以理解的。
接下来我们将神经网络的概念以严格术语进行表述。假设我们有三个输入特征$x_1,x_2,x_3$,这三个特征共同称为输入层(input layer),然后又四个隐藏单元(hidden units)共同称为隐藏层(hidden layer),一个输出神经元叫做输出层(output layer)。隐藏层之所以称之为隐藏,是因为不具备足够的事实依据或者训练样本值来确定这些隐藏单元。这是受到输入和输出层限制的,对输入输出我们所了解的基本事实就是$(x^{(i)},y^{(i)})$。
第一个隐藏单元需要输入特征$x_1,x_2,x_3$,然后输出一个记作$a_1$的输出值。我们使用字母$a$是因为这个可以表示神经元的“激活(activation)”的值。在这个具体的案例中,我们使用了一个单独的隐藏层,但实际上可能有多个隐藏层。假设我们用$a_1^{[1]}$来表示第一个隐藏层中的第一个隐藏单元。对隐藏层用从零开始的索引来指代层号。也就是输入的层是第$0$层,第一层隐藏层是第$1$层,输出层是第二层。再次强调一下,更复杂的神经网络就可能有更多的隐藏层。有了上述数学记号,第$2$层的输出就表达做$a_1^{[2]}$。统一记号就得到了:
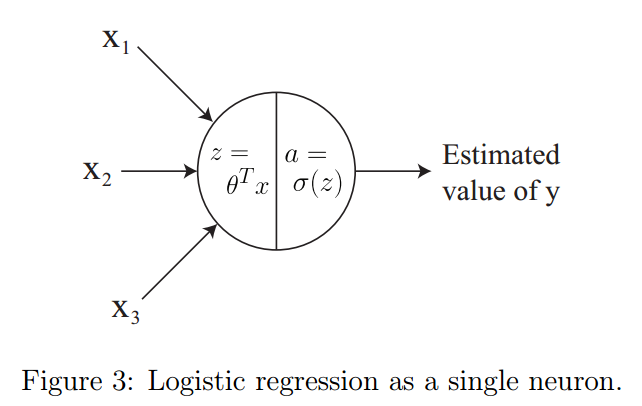
这里要说清的是,用方括号$[1]$上标的元素表示一切和第$1$层相关的,带圆括号的$x^{(i)}$表示的则是第$i$个训练样本,而$a^{[l]}_j$表示的是第$j$个单元在第$l$层的激活。可以将逻辑回归函数$g(x)$看做一个单个神经元(如图3所示):
向上面逻辑回归函数$g(x)$中输入的就是三个特征$x_1,x_2,x_3$,而输出的是对$y$的估计值。可以将上面这个$g(x)$表示成神经网络中的一个单个神经元。可以将这个函数拆解成两个不同的计算:$(1)z=w^Tx+b$;$(2)a=\sigma(z),\sigma(z)=\frac{1}{1+e^{-z}}$。要注意这里的记号上的差别:之前我们使用的是$z=\theta^Tx$但现在使用的是$z=w^Tx+b$,这里面的$w$是一个向量。后面的讲义中会看到如果是表示矩阵就用大写字母$W$了。这里的记号差别是为了遵循标准的神经网络记号。更通用的写法,还要加上$a=g(z)$,这里面这个$g(z)$可以试试某种激活函数。举几个例子,激活函数可以包括下面几种:
一般来说,$g(z)$都是非线性函数(non-linear function)。
回到前面的那个神经网络,第一隐藏层的第一个隐藏单元会进行下面的计算:
上式中的$W$是一个参数矩阵,而$W_1$指的是这个矩阵的第$1$行(row)。和第一个隐藏单元相关联的参数包括了向量$W_1^{[1]} \in R^3$和标量$b_1^{[1]} \in R^3$。对第$1$个隐藏层的第二和第三个隐藏单元,计算定义为:
其中每个隐藏单元都有各自对应的参数$W$和$b$。接下来就是输出层的计算:
上面式子中的$a^{[1]}$定义是所有第一层激活函数的串联(concatenation):
激活函数$a^{[2]}_1$来自第二层,是一个单独的标量,定义为$a^{[2]}_1=g(z^{[2]}_1)$,表示的是神经网络的最终输出预测结果。要注意对于回归任务来说,通常不用严格为正的非线性函数(比如ReLU或者Sigmoid),因为对于某些任务来说,基本事实$y$的值实际上可能是负值。
为了使用合理的计算速度来实现一个神经网络,我们必须谨慎使用循环(loops)。要计算在第一层中的隐藏单元的激活函数,必须要计算出来$z_1,...,z_4$和$a_1,...,a_4$。
最自然的实现上述目的的方法自然是使用for循环了。深度学习在机器学习领域中最大的特点就是深度学习的算法有更高的算力开销。如果你用了for循环,代码运行就会很慢。
这就需要使用向量化了。向量化和for循环不同,能够利用矩阵线性代数的优势,还能利用一些高度优化的数值计算的线性代数包(比如BLAS),因此能使神经网络的计算运行更快。在进行深度学习领域之前,小规模数据使用for循环可能就足够用了,可是对现代的深度学习网络和当前规模的数据集来说,for循环就根本不可行了。
接下来将的方法是不使用for循环来计算$z_1,...,z_4$。使用矩阵线性代数方法,可以用如下方法计算状态:
$$ \begin{aligned} \underbrace{ \begin{bmatrix} z^{[1]}_1 \ \vdots\ \vdots\ z^{[1]}4 \end{bmatrix} }{z^{[1]} \in R^{4\times 1}}
=\underbrace{ \begin{bmatrix}-&{W{[1]}_1}^T - \ -&{W{[1]}_2}^T -\&\vdots\ -&{W{[1]}4}^T -\end{bmatrix}}{W^{[1]}\in R^{4\times 3}}
\underbrace{ \begin{bmatrix}x_1\x_2\x_3 \end{bmatrix}}_{x\in R^{3\times 1}} +
\underbrace{ \begin{bmatrix} b^{[1]}_1 \ b^{[1]}_2 \ \vdots\ b^{[1]}4\end{bmatrix} }{b^{[1]}\in R^{4\times 1}}\quad\text{(2.4)} \end{aligned} $$
上面的矩阵下面所标注的$R^{n\times m}$表示的是对应矩阵的维度。直接用矩阵记号表示是这样的:$z^{[1]}= W^{[1]}x+b^{[1]}$。要计算$a^{[1]}$而不实用for循环,可以利用MATLAB/Octave或者Python里面先有的向量化库,这样通过运行分布式的针对元素的运算就可以非常快速的计算出$a^{[1]}=g(z^{[1]})$。数学上可以定义一个S型函数(sigmoid function)$g(z)$:
不够,这个S型函数不尽力针对标量(scalars)来进行定义,也可以对向量(vectors)定义。以MATLAB/Octave风格的伪代码,就可以如下方式定义这个函数:
上式中的$./$表示的是元素对除。这样有了向量化的实现后,$a^{[1]}=g(z^{[1]})$就可以很快计算出来了。
总结一下目前位置对神经网络的了解,给定一个输入特征$x\in R^3$,就可以利用$z^{[1]}=W^{[1]}x+b^{[1]}$和$a^{[1]}=g(z^{[1]})$计算隐藏层的激活,要计算输出层的激活状态(也就是神经网络的输出),要用:
$$\begin{aligned}
\underbrace{ z^{[2]} } _{ 1\times 1}
&=\underbrace{ W^{[2]} } _{ 1\times 4} \underbrace{ a^{[1]}} _{ 4\times 1} +\underbrace{ b^{[2]} } _{ 1\times 1}\quad,\quad \underbrace{ a^{[2]}} _{ 1\times 1}&=g(\underbrace{ z^{[2]} } _{ 1\times 1})\quad\text{(2.7)} \end{aligned} $$
为什么不对$g(z)$使用同样的函数呢?为啥不用$g(z)=z$呢?假设$b^{[1]}$和$b^{[2]}$都是零值的。利用等式$(2.7)$就得到了:
这样之前的$W^{[2]}W^{[1]}$就合并成了$\tilde W
假如你有了一个三个样本组成的训练集。每个样本的激活函数如下所示:
$$ \begin{aligned} z^{1} &= W^{[1]}x^{(1)}+b^{[1]}\ z^{1} &= W^{[1]}x^{(2)}+b^{[1]}\ z^{1} &= W^{[1]}x^{(3)}+b^{[1]}\ \end{aligned} $$
要注意上面的括号是有区别的,方括号[]内的数字表示的是层数(layer number),而圆括号()内的数字表示的是训练样本编号(training example number)。直观来看,似乎可以用一个for循环实现这个过程。但其实也可以通过向量化来实现。首先定义:
注意,我们是在列上排放训练样本而非在行上。然后可以将上面的式子结合起来用单个的统一公式来表达:
$$ Z^{[1]}=\begin{bmatrix} |&|&|&\ z^{1}&z^{1}&z^{1}\ |&|&|&\ \end{bmatrix} =W^{[1]}X+b^{[1]}\quad\text{(2.14)} $$
你或许已经注意到了我们试图在$W^{[1]}X \in R^{4\times 3}$的基础上添加一个$b^{[1]}\in R^{4\times 1}$。严格按照线性代数规则的话,这是不行的。不过在实际应用的时候,这个加法操作是使用广播(boradcasting)来实现的。创建一个中介$\tilde b^{[1]}\in R^{4\times 3}$:
然后就可以计算:$Z^{[1]}= =W^{[1]}X+\tilde b^{[1]}$。通常都没必要去特地构建一个$\tilde b^{[1]}$。检查一下等式(2.14),你就可以假设$b^{[1]}\in R^{4\times 1}$能够正确广播(broadcast)到$W^{[1]}X \in R^{4\times 3}$上。
综上所述:假如我们有一个训练集:$(x^{(1)},y^{(1)}),...,(x^{(m)},y^{(m)})$,其中的$x^{(i)}$是一个图形而$y^{(i)}$是一个二值化分类标签,标示的是一个图片是否包含一只猫(比如y=1就表示是一只猫)。
首先要将参数$W^{[1]},b^{[1]},W^{[2]},b^{[2]}$初始化到比较小的随机值。对每个样品,都计算其从$S$型函数(sigmoid function)$a^{2}$的输出概率。然后利用逻辑回归(logistic regression)对数似然函数(log likelihood):
$$ \sum^m_{i=1}(y^{(i)}\log a^{2} +(1-y^{(i)}\log(1-a^{2})\quad\text{(2.16)} $$
最终,利用梯度上升法(gradient ascent)将这个函数最大化。这个最大化过程对应的就是对神经网络的训练。
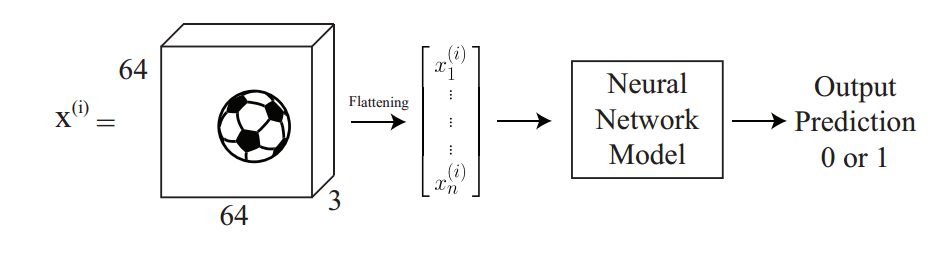
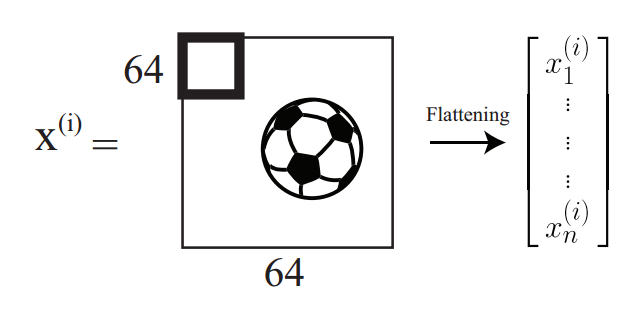
现在我们不再使用上面的房价预测的例子,要面对一个新问题了。假如我们要检测在一个图片中是否包含足球。给定一张图片$x^{(i)}$作为输入,我们希望能够输出一个二值化的预测,如果图中包含足球就输出$1$,反之就输出$0$。
备注:图像可以表示成一个矩阵的形式,矩阵的元素等于图像的像素数。不过彩色的图像是以张量/体积(volume)的形式来进行数字化表示的(也就是说有三个通道,或者说是三个矩阵堆叠到一起)。这里有三个矩阵是对应着显示器上面的三原色红绿蓝(RGB)的值。在下面的案例中,我们有一个$64\times 64\times 3$数值规模的图像,其中包含了一个足球。拉平(flattened)之后就成了一个单独的向量,包含有$12288$个元素。
一个神经网络模型包含两个成分:$(i)$网络结构,定义了有多少层,多少个神经元,以及多少个神经元彼此链接;$(ii)$参数(数值values;也称作权重weights)。在这一节,我们要讲一下如何学习这些参数。首先我们要讲一下参数初始化和优化,以及对这些参数的分析。
设想一个双层神经网络。左侧的输入是一个拉平的图像向量$x^{(1)},...,x^{(n)}$。在第一个隐藏层中,要注意所有的输入如何连接到下一层中的所有神经元上。这就叫做全连接层(fully connected layer)。
下一步就是计算在这个神经网络中有多少个参数。一种方法是手动向前计算(forward propagation by hand)。
已知其中的$z^{[1]},a^{[1]}\in R^{3\times 1}, z^{[2]},a^{[2]}\in R^{2\times 1},z^{[3],a^{[3]}\in R^{1\times 1}}$。现在不知道的就是$W^{[1]}$的规模。不过这个可以算出来。
已知$x\in R^{n\times 1}$。因此则有:
根据矩阵乘法,可以推断出上面式子中的$?\times ?$应该是$3\times n$。另外还能推断出基(原文写的bias莫不是偏差?)的规模应该是$3\times 1$,因为必须能够匹配$W^{1]}x^{(i)}$。对每个隐藏层重复上面的这一过程。这样就得到了:
加到一起,就知道在第$1$层是$3n+3$,第$2$层是$2\times 3+2$,第$3$层就是$2+1$。这样参数一共就是$3n+14$个。
在我们开始训练神经网络之前,必须先对上面这么多参数赋予初始值。这里不能使用零值作为初始值。因为第一层的输出这样就总是相同的了,因为$W^{[1]}x^{(i)}+b^{[1]}=0^{3\times1}$,其中的$0^{3\times1}$表示的是全部值为零的形状为$n\times m$的矩阵。这样会给后续的参数更新带来麻烦(也就是所有的梯度都是相同的)。解决办法是对所有参数以极小的随机值来进行初始化(比如一般可以使用在0附近正态分布的值$\mathcal{N}(0,0.1)$)。单输出时候了之后,就可以开始利用梯度下降法(gradient descent)来开始训练这个神经网络了。
训练过程中接下来的一步就是更新参数。在通过整个神经网络的一次正向过程之后,输出就是一个预测值$\hat y$。可以计算损失函数$\mathcal{L}$,这个案例中我们使用对数损失函数(log loss):
上面的损失函数$\mathcal{L}(\hat y,y)$就会产生单个的一个表两只。简单起见,我们将这个损失函数值也记作$\mathcal{L}$。有了这个值,就必须对神经网络中各层的所有参数进行更新。对任意的一个给定的层次$l$,更新方法如下所示:
上式中的$\alpha$是学习速率(learning rate).另外还必须计算对应参数的梯度:$\frac{\partial \mathcal{L}}{\partial W^{[l]}}$和$\frac{\partial \mathcal{L}}{\partial b^{[l]}}$.
要记住,上面是决定了不去将所有参数都设置为零值。那么如果就是全部用零值来初始化会怎么样?我明知道$z^{[3]}=w^{[3]}a^{[2]}+b^{[3]}$会等于零,因为$W^{[3]}$和$b^{[3]}$都是零值了。不过神经网络的输出则定义成$a^{[3]}=g(z^{[3]})$。还记得上面的$g(\cdot)$的定义是一个S型函数(sigmoid function)。这就一诶这$a^{[3]}=g(z^{[3]})=0.5$。也就是不论提供什么样的$x^{(i)}$的值,网络的输出都将会是$\hat y=0.5$。
要是我们将所有参数都用非零值但是都是同一个值来初始化会怎么样?这时候,考虑第1层的激活状态函数:
如此一来激活向量$a^{[1]}$的每一个元素都是相同的(因为$W^{[1]}$包含的是全部相同的值)。这一情况也会发生在神经网络中的其他所有层上。结果就是,在计算题度的时候,一个层里面的所有神经元对最终的损失函数都具有同等的贡献。这个性质叫做对称(symmetry)。这就意味着(一个层内)的每个神经元都接受完全相同的梯度更新至(也就是所有的神经元都进行同样的学习)。
在实践中,会有一种比随机值初始化更好的方法。叫做Xavier/He 初始化,对权重(weights)进行的初始化如下
上式中的$n^{[l]}$表示的是第$l$层的神经元个数。这种操作是一种最小规范化技术(mini-normalization technique)。对于单层而言,设该层的输入(input)的方差(variance)是$\sigma^{(in)}$而输出(也就是激活状态函数,activations)的方差是$\sigma^{(out)}$.Xavier/He 初始化就是让$\sigma^{(in)}$尽量接近$\sigma^{(out)}$。
回忆一下咱们这个神经网络的参数:$W^{[1]},b^{[1]},W^{[2]},b^{[2]},W^{[3]},b^{[3]}$。要对这些进行更新,可以利用等式$(3.10)$和$(3.11)$里面的更新规则来实现随机梯度下降(stochastic gradient descent,缩写为SGD)。首先计算对应$W^{[3]}$的梯度。这是因为$W^{[1]}$对损失函数的影响比$W^{[3]}$更复杂。这是由于在计算的次序上来说,$W^{[3]}$更接近(closer)输出$\hat y$。
注意上面用的函数$g(\cdot)$是S型函数(sigmoid)。质疑函数的导数(derivative)是$g'=\sigma'=\sigma(1-\sigma)$。另外有
接下来要计算$W^{[2]}$的梯度。这里不再推导$\frac{\partial \mathcal{L}}{\partial W^{[2]}}$,可以利用微积分里面的链式规则(chain rule)。已知$L$依赖于$\hat y=a^{[3]}$。
如果观察正向传播(forward propagation),就知道$\mathcal{L}$依赖于$\hat y=a^{[3]}$。利用链式规则就可以插入$\frac{\partial a^{[3]}}{\partial a^{[3]}}$:
我们已知$a^{[3]}$和$z^{[3]}$直接相关。
接下来,我们知道$z^{[3]}$和$a^{[2]}$直接相关。要注意不能使用$W^{[2]}$或者$b^{[2]}$,因为$a^{[2]}$十字等式$(3.5)$和$(3.6)$之间唯一的共有元素(common element)。在反向传播(Backpropagation)中需要用共有元素。
再次用到$a^{[2]}$和$z^{[2]}$直接相关,而$z^{[2]}$直接依赖于$W^{[2]}$,这使得我们可以计算整个链:
回忆一下之前的$\frac{\partial \mathcal{L}} {\partial W^{[3]}}$:
因为我们首先计算出了$\frac{\partial \mathcal{L}} {\partial W^{[3]}}$,就知道了$a^{[2]}= \frac{\partial z^{[3]}} {\partial W^{[3]}}$。类似地就也有$(a^{[3]}-y)=\frac{\partial \mathcal{L}} {\partial W^{[3]}}$。这些可以帮我们计算出$\frac{\partial \mathcal{L}} {\partial W^{[2]}}$。将这些值带入到等式$(3.26)$。这就得到了:
$$
\frac{\partial L}{\partial W^{[2]}} =
\underbrace{ \frac{\partial L}{\partial a^{[3]}} \frac{\partial a^{[3]}}{\partial z^{[3]}} }_{(a^{[3]}-y)}
\underbrace{
\frac{\partial z^{[3]}} {\partial a^{[2]}}
}_{W^{[3]}}
\underbrace{
\frac{\partial a^{[2]}} {\partial z^{[2]}}
}_{g'(z^{[2]})}
\underbrace{ \frac{\partial z^{[2]}}{\partial W^{[2]}} }_{a^{[1]}}
=(a^{[3]}-y)W^{[3]}g'(z^{[2]})a^{[1]} \quad \text{(3.28)} $$
虽然已经大幅度简化了这个过程,但还没有完成。因为要计算更高维度的导数(derivatives),要计算等式$(3.28)$所要求的矩阵乘法的确切的次序(order)还不清楚。必须在等式$(3.28)$中对各个项目进行重排列,使其维度相符合(align)。首先将每个项目的维度标记出来:
\underbrace{ (a^{[3]}-y) }_{1\times1}
\underbrace{ W^{[3]} }_{1\times2}
\underbrace{ g'(z^{[2]}) }_{2\times1}
\underbrace{ a^{[1]} }_{3\times1} \quad \text{(3.29)} $$
要注意上面各项目并没有根据形状进行妥善排列。因此必须利用矩阵线性代数的形制将其重排列,使矩阵运算能够产生一个有正确形态的输出结果。正确的排序如下所示:
\underbrace{ {W^{[3]}}^T }_{2\times1}
\circ
\underbrace{ g'(z^{[2]}) }_{2\times1}
\underbrace{ (a^{[3]}-y) }_{1\times1}
\underbrace{ {a^{[1]}}^T }_{1\times3} \quad \text{(3.30)} $$
其余的梯度计算就作为练习交给读者自行完成了。在计算剩余参数的梯度的嘶吼,利用已经计算的$\frac{\partial \mathcal{L}}{\partial W^{[2]}}$和$\frac{\partial \mathcal{L}}{\partial W^{[3]}}$作为中介结果是很重要的,因为这两者都可以直接用于梯度计算中。
回到优化上,我们之前讨论过随机梯度下降法(stochastic gradient descent,缩写为SGD)了。接下来要将的是梯度下降(gradient descent)。对任意一个单层$l$,更新规则的定义为:
上式中的$J$是成本函数(cost function)$J=\frac{1}{m}\sum^m_{i=1}L^{(i)}$,而其中的$L^{(i)}$是对单个样本的损失函数值(loss)。梯度下降更新规则和随机梯度下降更新规则的区别是成本函数$j$给出的是更精确的梯度,而损失函数$L^{(i)}$可能是有噪音的。随机梯度下降法视图从全部梯度下降中对梯度进行近似。梯度下降的弱点是很难在依次向前或向后传播阶段(phase)中计算所有样本的所有状态函数。
在实践中,研究和应用一般都使用小批量梯度下降(mini-batch gradient descent)。这个方法是梯度下降和随机梯度下降之间的一个折中方案。在这个方法中,成本函数$J_{mb}$定义如下:
上式中的$B$是指最小批量(mini-batch)中的样本数目。
还有一种优化方法叫做动量优化(momentum optimization)。设想最小批量随机梯度下降。对于任意个单一层$l$,更新规则如下所示:
注意这里的更新规则有两步,而不是之前的单步了。权重(weight)的更新现在依赖于在这一更新步骤的成本函数$J$以及速度(velocity)$v_{dW^{[l]}}$。相对重要程度(relative importance)受到$\beta$的控制。设想模拟一个人开车。在懂得时候,汽车有栋梁(momentum)。如果踩了刹车或者油门,汽车由于有动量会继续移动。回到优化上,速度(velocity)$v_{dW^{[l}}$就会在时间上跟踪梯度。这个技巧对训练阶段的神经网络有很大帮助。
这时候已经初始化过参数了,并且也优化出了这些参数。加入我们对训练出来的模型进行应用评估发现在训练集商贸能够达到96%的准确率,但在测试集上准确率只有64%。解决的思路包括:收集更多数据,进行规范化,或者让模型更浅(shallower)。下面简单讲解一下规范化的技术。
设下面的$W$表示的是一个模型中的所有参数。在神经网络中,你可能会想到对所有层权重$W^{[l]}$添加第二项。为了简单,就简写成$W$。对成本函数进行$L2$规范化街上另一项就得到了:
上式中的$J$是前文提到过的标准成本函数,$\lambda$是一个任意值,越大表示更加规范化,而$W$包含所有的权重矩阵(weight matrices),等式$(3.34)(3.35)(3.36)$是完全等价的。这样L2规范化的更新规则就成了:
$$
\begin{aligned}
W &= W-\alpha\frac{\partial J}{\partial W} -\alpha\frac{\lambda}{2} \frac{\partial W^TW}{\partial W} \quad\text{(3.37)} \
&= (1-\alpha\lambda)W-\alpha \frac{\partial J}{\partial W} \quad\text{(3.38)} \
\end{aligned}
$$
当使用梯度下降更新参数的时候,并没有$(1-\alpha\lambda)W$这一项。这就意味着通过L2规范化,每个更新会泽都会加入某一个惩罚项(penalization),这个惩罚项依赖于$W$。这个惩罚项(penalization)会增加成本函数(cost)$J$的值,这样可以鼓励单个参数值在程度上(in magnitude)尽量缩小,这是一种降低过拟合(overfitting)发生概率的办法。
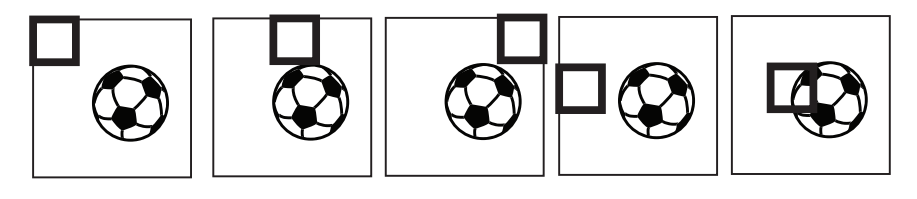
回忆一下逻辑回归(logistic regression)。也可以表示成一个神经网络,如图3所示。参数向量$\theta = (\theta_1,...,\theta_n)$必须和输入向量$x=(x_1,...,x_n)$有同样的元素个数。在检测图像中是否包含足球这个例子中,这就意味着$\theta_1$必须总要查看图像的左上角的像素。不过我们知道足球可能出现在图像的任意一个区域而不一定总在中心位置。很可能$\theta_1$从没被选镰刀图片左上角有足球。结果就是在测试的时候,只要一个图像中足球出现在左上角,逻辑回归就很可能预测没有足球。这就是个问题了。
因此我们就要试试卷积神经网络(convolutional neural networks)。设$\theta$不再是一个向量而本身就是一个矩阵。比如在足球这个样例中,设$\theta=R^{4\times4}$。
为了简单起见,我们展示一个$64\times 64$的图像但还记得图像实际上是三维的包含了三个通道。现在将参数矩阵$\theta$分散(slide)在图像上。这就如上图中所示在图像左上角位置的加粗方框。要计算激活函数$a$,就要计算$\theta$和$x_{1:4,1:4}$按元素求积(element-wise product),其中x的下标表示的是从图像x的左上方$4\times4$个像素中取值。然后将按元素求积得到的所有元素加到一起来将矩阵压缩(collapse)成一个单独标量。具体形式为:
然后将这个窗口向图像右侧轻微移动,然后重复上面的国产。一旦到达了行尾了,就从第二行的开头部位开始。
一旦到达了图像末尾,参数$\theta$就已经"检视"过了图片的全部像素了:$\theta_1$就不再只是和左上像素相关联了。结果就是,如论足球出现的位置是图像的右下角或者左上角,神经网络都可以成功探测到。