Skip to content

Latest commit

 

History

History
169 lines (135 loc) · 4.2 KB

2、Python实现线性回归.md

File metadata and controls

169 lines (135 loc) · 4.2 KB
Raw

Python实现线性回归

完整代码与数据见：https://github.com/xiaohuzai/ML-Excercise.git

导入数据

import numpy as np
data = np.loadtxt('linear_regression_data1.txt',delimiter=',')
X = np.c_[np.ones(data.shape[0]),data[:,0]]
y = np.c_[data[:,1]]

data:

6.1101 17.592 5.5277 9.1302 8.5186 13.662 7.0032 11.854 5.8598 6.8233 8.3829 11.886 7.4764 4.3483 8.5781 12 6.4862 6.5987 5.0546 3.8166......

X:

1 6.1101 1 5.5277 1 8.5186 1 7.0032 1 5.8598 1 8.3829 1 7.4764 1 8.5781 1 6.4862 1 5.0546......

y:

17.592 9.1302 13.662 11.854 6.8233 11.886 4.3483 12 6.5987 3.8166......

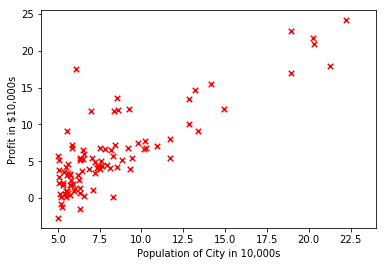
显示数据

import matplotlib.pyplot as plt
plt.scatter(X[:,1], y, s=30, c='r', marker='x', linewidths=1)
plt.xlim(4,24)
plt.xlabel('Population of City in 10,000s')
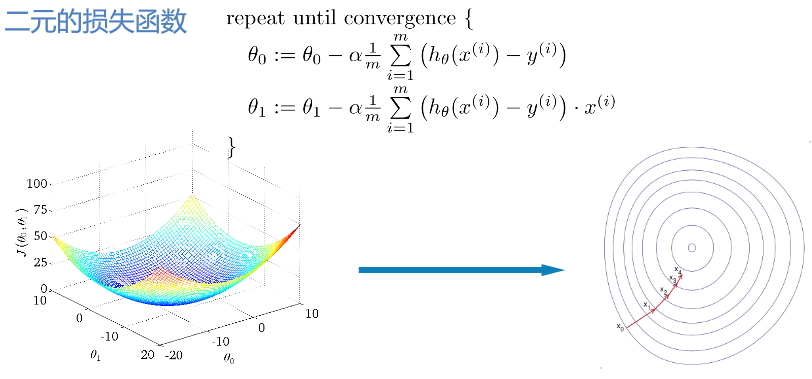
plt.ylabel('Profit in $10,000s')

计算损失函数

# theta默认值为[0,0]T
def computerCost（X,y,theta=[[0],[0]]）:
    m = y.size
    J = 0
    # X点乘theta
    h = X.dot(theta)
    J = 1.0/(2*m)*(np.sum(np.squre(h-y)))
# theta默认值为[0,0]T时损失函数的值
computerCost(X,y)
Out[15]: 32.072733877455676

梯度下降函数

# 默认迭代次数为1500次，学习率alfa取0.01
def gradientDescent(X, y, theta=[[0],[0]], alpha=0.01, num_iters=1500):
    m = y.size
    # J_history用来保存每一次迭代后损失函数J的值
    J_history = np.zeros(num_iters)
    # 迭代的过程
    for iter in np.arange(num_iters):
        h = X.dot(theta)
        theta = theta - alpha*(1.0/m)*(X.T.dot(h-y))
        J_history[iter] = computeCost(X, y, theta)
    return(theta, J_history)
# 计算迭代1500次以后theta的值
theta , Cost_J = gradientDescent(X, y)
theta
Out[27]: 
array([[-3.63029144],
       [ 1.16636235]])
# 即theta0 = -3.63029144，theta1 = 1.16636235
# 画出每一次迭代和损失函数变化
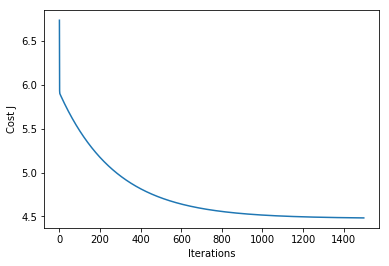
plt.plot(Cost_J)
plt.ylabel('Cost J')
plt.xlabel('Iterations')

可见在迭代了1500次以后，损失函数J的值趋近收敛。

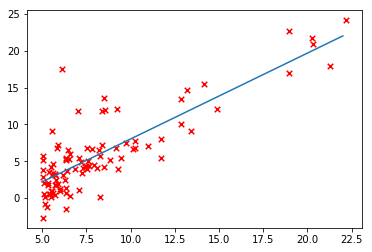
画图

# 画出我们自己写的线性回归图
xx = np.arange(5,23)
yy = theta[0]+theta[1]*xx
plt.scatter(X[:,1], y, s=30, c='r', marker='x', linewidths=1)
plt.plot(xx,yy, label='Linear regression (Gradient descent)')

# 和Scikit-learn中的线性回归对比一下 
from sklearn.linear_model import LinearRegression
# 我们自己梯度下降计算得到的线性回归
xx = np.arange(5,23)
yy = theta[0]+theta[1]*xx
plt.scatter(X[:,1], y, s=30, c='r', marker='x', linewidths=1)
plt.plot(xx,yy, label='Linear regression (Gradient descent)')
# 使用Scikit计算得到的线性回归
regr = LinearRegression()
regr.fit(X[:,1].reshape(-1,1), y.ravel())
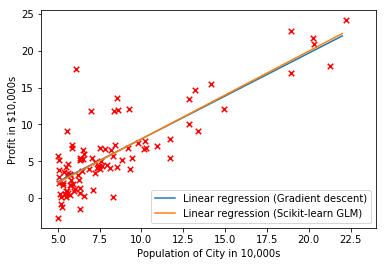
plt.plot(xx, regr.intercept_+regr.coef_*xx, label='Linear regression (Scikit-learn GLM)')

plt.xlim(4,24)
plt.xlabel('Population of City in 10,000s')
plt.ylabel('Profit in $10,000s')
plt.legend(loc=4)

可以看出两者基本重合。

预测

使用我们计算得到的线性回归模型，预测一下人口为35000和70000的城市的结果。

print(theta.T.dot([1, 3.5])*10000)
[ 4519.7678677]
print(theta.T.dot([1, 7])*10000)
[ 45342.45012945]